0x00前言
考试终于考完了,假期就来天天坑了吧,本次补上基本的几个排序方法,堆排序、快速排序、选择排序插入排序
0x01 插入排序
直接插入排序时一种最简单的排序方法,它的基本操作时将一个记插入到以排好序的有序表中,从而得到一个新的、记录增加 1的有序表。
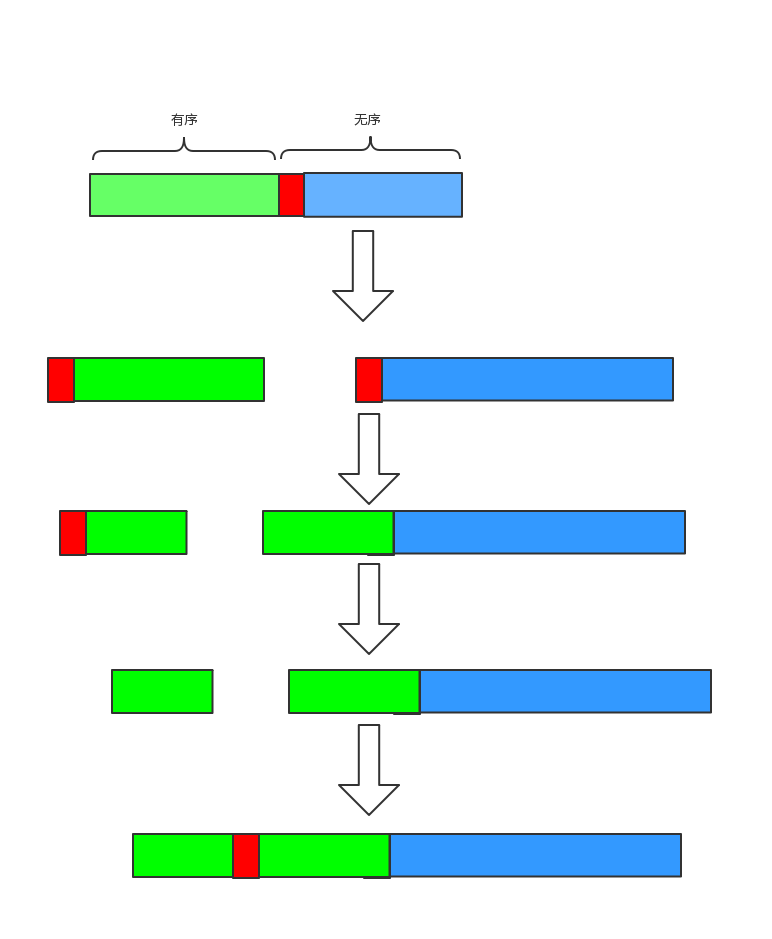
例如:
初始序列 : [12] 15 09 20 06 36 28
第1趟结果: [12 15] 09 20 06 36 28
第2趟结果 [09 12 15] 20 06 36 28
第3趟结果: [09 12 15 20] 06 36 28
第4躺结果: [06 09 12 15 20] 36 28
第5趟结果: [06 09 12 15 20 36] 28
第6趟结果: [06 09 12 15 20 28 36]
代码为
typedef struct{
int r[MAXSIZE + 1];
int length;
}SqList;
void InsertSort(SqList &L){
// 对顺序表L作直接插入排序
for(int i=2; i<=L.length;i++){
if(L.r[i]<=L.r[i-1]){
L.r[0]=L.r[i] // 缓存
L.r[i]=L.r[i-1];
for(int j=i-2;L.r[0]<L.r[j]; j--) L.r[j+1] = L.r[j];
L.r[j+1]=L.r[0];
}
}
}
其时间复杂度为
最好情况(正序): 时间复杂度O(n) 比较次数:n-1 移动次数:0
最坏情况(逆序):时间复杂度O(n2)
折半插入排序
由于插入排序的基本操作是在一个有序表中进行查找和插入,则这个"查找"操作可利用"折半查找"来实现,由此进行的插入排序称之为折半插入排序,其算法为
void BInsertSort(SqList &L){
// 对顺序表L作折半插入排序
for(int i=2;i<=L.length;++i){
L.r[0]=L.r[0]; // 将L.r[i]暂存到L.r[0]
int low=l;
int high = i-1;
while(low <=high){
int m=(low+high)/2; //折半
if(LT(L.r[0].key, L.r[m].key)) high = m-1; //插入点在低半区
else low = m+1; // 折半点在高半区
}//while
for(int j=i-1;j>=high+`;--j) L.r[j+1] = L.r[j]; // 记录后移
L.r[high+1] = L.r[0];
}// for
}//BInsertSort
2-路插入排序
2-路插入排序是在折半插入排序的基础上再加改进,其目的是减少排序过程中的移动记录的次数,但为此需要n个记录的辅助空间。具体做法是:另设一个和L.r同类型的数据组d,首先将L.r[1]赋值给d[1],并将d[1]看成是在排好序的序列中处于中间位置的记录,然后从L.r中第2个记录起依此插入到d[1]之前或之后的有序序列中。先将待插记录的关键字和d[1]的关键字进行比较,若L.r[i].key<d[1].key,则将L.r[i]插入到d[1]之前的有序表中。反之,则将L.r[i]插入到d[1]之后的有序表中。
#define SIZE 100 //静态链表容量
typedef struct {
RcdType rc; //记录项
int next; // 指针项
}SLNode; // 表结点类型
typedef struct {
SLNode r[SIZE]; // 0号单元为表头结点
int length; // 链表当前长度
}SLinkListType; // 静态链表类型
void Arrange(SLinkistType &SL){
// 根据静态链表SL中各节点的指针值调整记录位置,使得SL中记录按关键字非递减
//有序排列
p= SL.r[0].next; // p指示第一个记录的当前位置
for(int i=1;i<SL.length;++i){
while(p<i) p=SL.r[p].next; //找到第i个记录,并用p指示其在SL中当前的位置
q = SL.r[p].next; // q指示尚未调整
if(p!=i }{
SLinkListType &temp;
temp.r[0]=SL.r[p];
SL.r[p] = SL.r[i]; //交换记录
SL.r[i]=temp.r[0];
SL.r[i].next = p ;
}
p=q;
}//Arrange
0x02快速排序
首先冒泡排序的过程是。首先将第一个记录的关键字和第二个记录的关键字进行比较,若为逆序(即L.r[1].key > L.r[2].key),则将两个记录交换之,然后比较第二个记录和第三个记录的关键字。依此类推,直至第n-1个记录和第n个记录的关键字进行过对比个记录的位置上。然后进行第二趟起泡排序,对前n-1个记录进行同样操作,其结果是是其关键字次大的记录被安置到第n-1个记录的位置上。
typedef struct{
int r[MAXSIZE + 1];
int length;
}SqList;
void BubbleSort(SqList &L){
for(int i=1,change=TRUE; i<L.length;i++){
change = FALSE;
for(int j=1;j<=L.length - i;j++){
if(L.r[j] > L.r[j+1])
{
L.r[0] = L.r[j];
L.r[j] = L.r[j+1];
L.r[j+1] = L.r[0];
change = TRUE;
}
}
}
}
冒泡排序的时间复杂度为
最好情况(正序): 时间复杂度O(n)
最坏情况(逆序): 时间复杂度O(n2)
快速排序是对冒泡排序的一种改进,它的基本思想是,通过一趟排序将待排序记录分割成独立的两部分,其中一部分记录的关键字均比另一部记录的关键字小,则可分别对这两部分记录继续进行排序,以达到整个序列有序。首先选一个枢轴,通过一趟排序将待排序记录分割成独立的两部分,前一部分记录的关键字均小于或等于枢轴,后一部分记录的关键字均大于或等于枢轴,然后分别对这两部分重复上述的方法,知直到整个序列有序。快速排序是平均性能最好的内部排序算法。
一轮排序的使用图片为
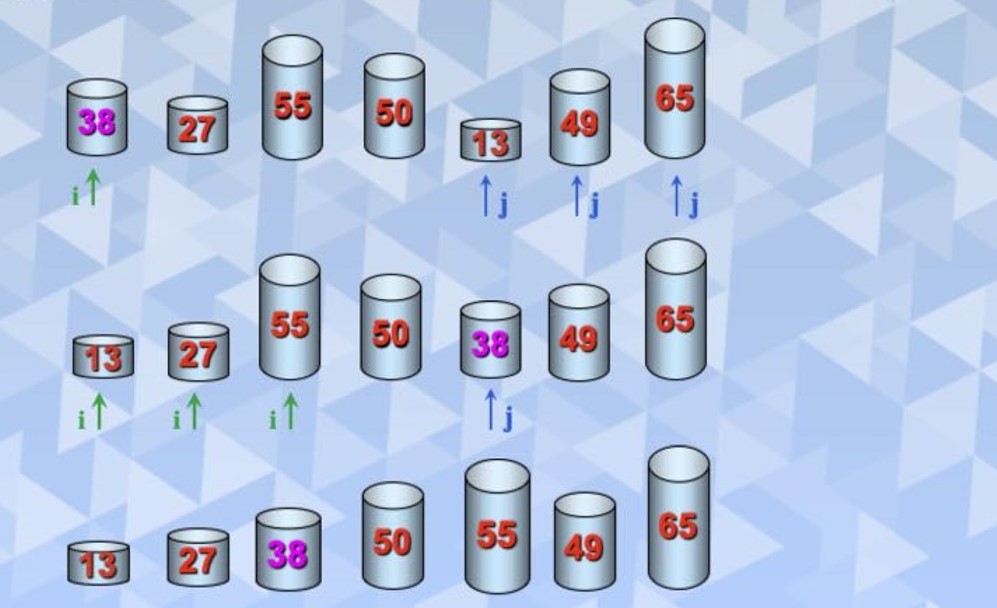
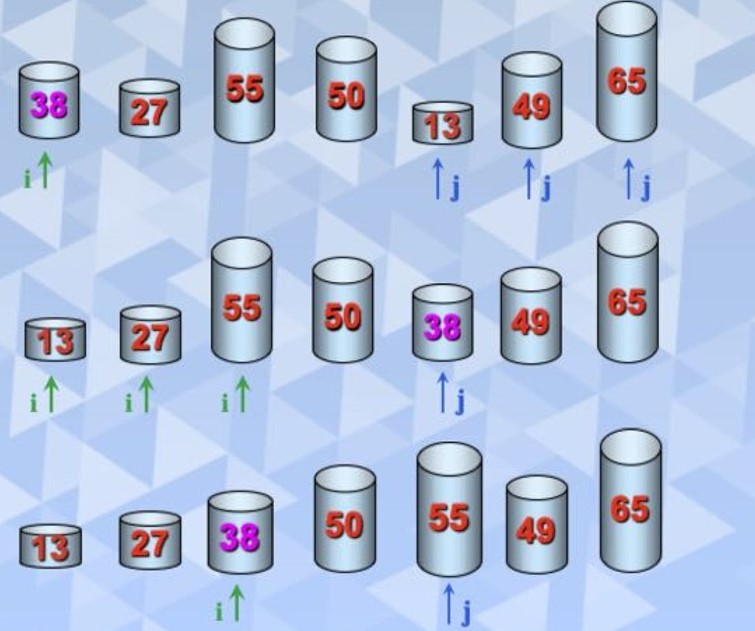
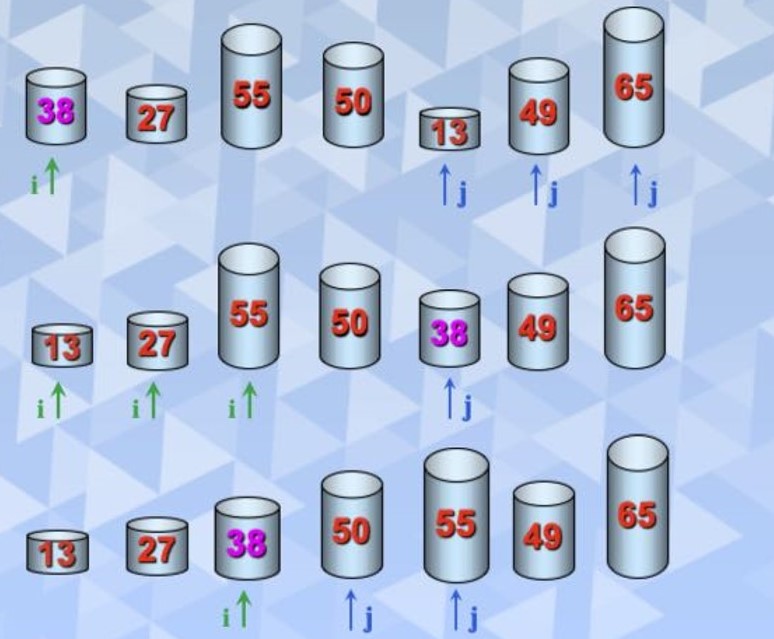

typedef struct{
int r[MAXSIZE + 1];
int length;
}SqList;
int Partition(SqList &L, int low , int high){
L.r[0] = L.r[low];
while(low< high){
while(low < high && L.r[high]>=L.r[0]) high--;
if(low<high) L.r[low++] = L.r[high];
while(low<high && L.r[low] <=L.r[0]) low++;
if(low < high) L.r[high--] = L.r[low];
}
L.r[low] = L.r[0];
return low;
}
void QSort(SqList &L, int low ,int high){
if(low<high)
{
int pivotloc;
pivotloc = Partition(L, low, high);
QSort(L, low, pivotloc-1);
QSort(L. pivotloc+1, high);
}
}
其时间复杂度
最好情况:每一次划分对一个记录后,该记录的左侧子表与右侧子表的长度相同。
时间复杂度O(n log2 n)
最坏情况(有序或者基本有序):每次划分只得到一个比上一次划分少一个记录的子序列,另一个子序列为空。这时候已经退化为冒泡排序
时间复杂度O(n2)
快速排序是一种不稳定的排序算法
0x03 堆排序
堆的定义为:n个元素的序列{k1,k2,...,kn}当且仅当满足下列关系时称为堆
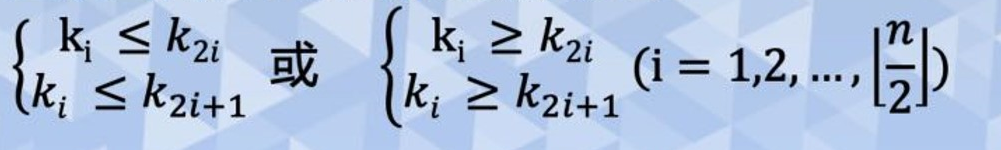
堆是具有下列性质的完全二叉树:每个结点的值都小于或等于其左右孩子结点的值(称为小顶堆),或每个结点的值都大于或等于其左右孩子的结点的值(称为大顶堆),其图解为

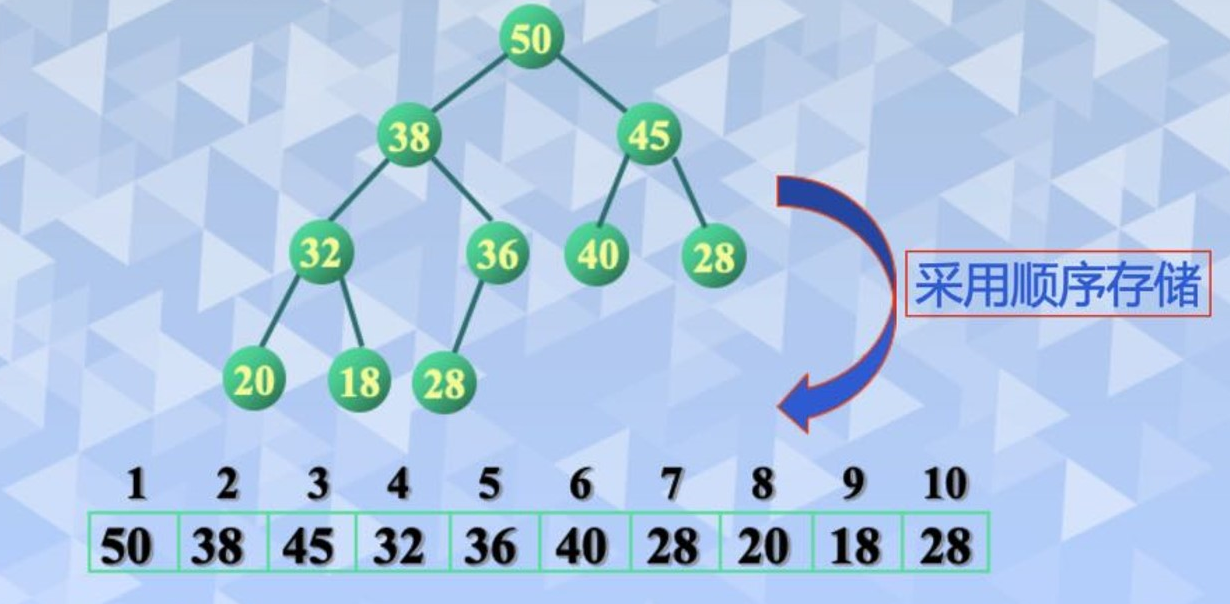
基本思想为:首先将待排序的记录序列构造成一个大顶堆,此时,选出了堆中所有记录的最大值,然后将其输出,并将剩余的记录再调整为大顶堆,这样又找出了次大的记录,依此类推,直到堆中只有一个记录
typedef struct{
int r[MAXSIZE + 1];
int length;
}SqList;
void HeapAdjust(SqList &L, int s, int m){
//待调整序列L.r[s..m]中除了L.r[s]外的记录均满足大顶堆的定义
L.r[0] = L.r[s];
for(int j=2*s;j<=m;j*=2){
if(j<m && L.r[j] < L.r[j+1]) j++;
if(L.r[0] > L.r[j]) break;
L.r[s] = L.r[j];
s=j;
}
L.r[s] = L.r[0];
}
void HeapSort(SqList &L){
for(int i=L.length/2; i>0;i--){ // 构造堆
HeapAdjust(L, i, L.length);
for(int i=L.length; i>1; i--){
int temp;
temp = L.r[1];
L.r[1] = L.r[i];
L.r[i] = temp; // 输出堆顶
HeapAdjust(L, 1, i-1); //调整堆
}
}
}
时间复杂度
堆排序的最好、最坏和平均时间复杂度均为O(n log2 n) 堆排序只需要一个辅助空间L.r[0]
堆排序是一种不稳定的排序算法
Reference
- 数据结构 C语言版 清华大学出版社