数据结构(二)之木林森

  数据结构

0x00前言

树型结构式一类重要的非线性数据结构，其中以树和二叉树最为常用。

0x01 二叉树概念

二叉树是另一种属性结构，他的特点是每个结点至多只有两棵子树(即二叉树中不存在度大于2的结点)，并且二叉树的子树有左右之分，其次序不能任意颠倒.

  • 一颗深度为k且有2k -1个结点的二叉树称为满二叉树
  • 在二叉树的第i层上至多有个结点2i-1(i>=1)

图a为满二叉树，图b为完全二叉树，其余的为非完全二叉树

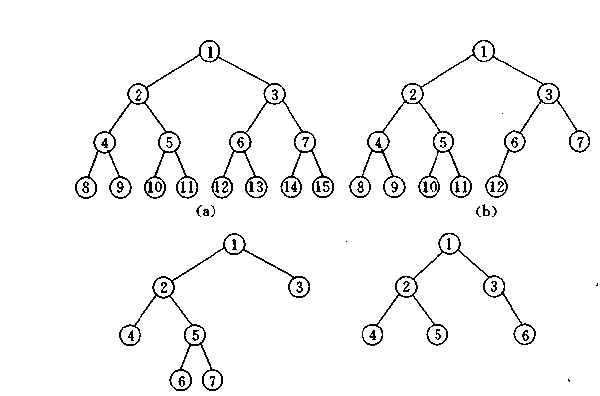
C语言代码的二叉树二叉存储表存储表式为:

typedef struct BiTNode{
    TElemType    data;
    strcut BiTNode  *lchild,&rchild;// 左右孩子指针
}

0x02遍历二叉树

先序遍历二叉树

若二叉树为空，则空操作;否则

  1. 访问根节点;
  2. 先序遍历左子树
  3. 先序遍历右子树

代码如下:

template <typename T, typename VST> // 元素类型、操作器
void travePre_R( BinNodePosi(T) x, VST& visit) { //二叉树先序遍历算法
    if (!x) return;
    visit( x-> data );
    travePre_R( x->lc, visit );
    travePre_R( x->rc, visit );
}

中序遍历二叉树

若二叉树为空，则空操作;否则

  1. 中序遍历左子树
  2. 访问根节点
  3. 中序遍历右子树

代码为:

template <typename T, typename VST> // 元素类型、操作器
void travePre_R( BinNodePosi(T) x, VST& visit) { //二叉树中序遍历算法
    if (!x) return;
    travePre_R( x->lc, visit );
    visit( x-> data );
    travePre_R( x->rc, visit );
}

后序遍历二叉树

若二叉树为空，则空操作;否则

  1. 后序遍历左子树
  2. 后序遍历右子树
  3. 访问根节点

代码如下:

template <typename T, typename VST> // 元素类型、操作器
void travePre_R( BinNodePosi(T) x, VST& visit) { //二叉树后序遍历算法
    if (!x) return;
    travePre_R( x->lc, visit );
    travePre_R( x->rc, visit );
    visit( x-> data );
}

例：有如下二叉树

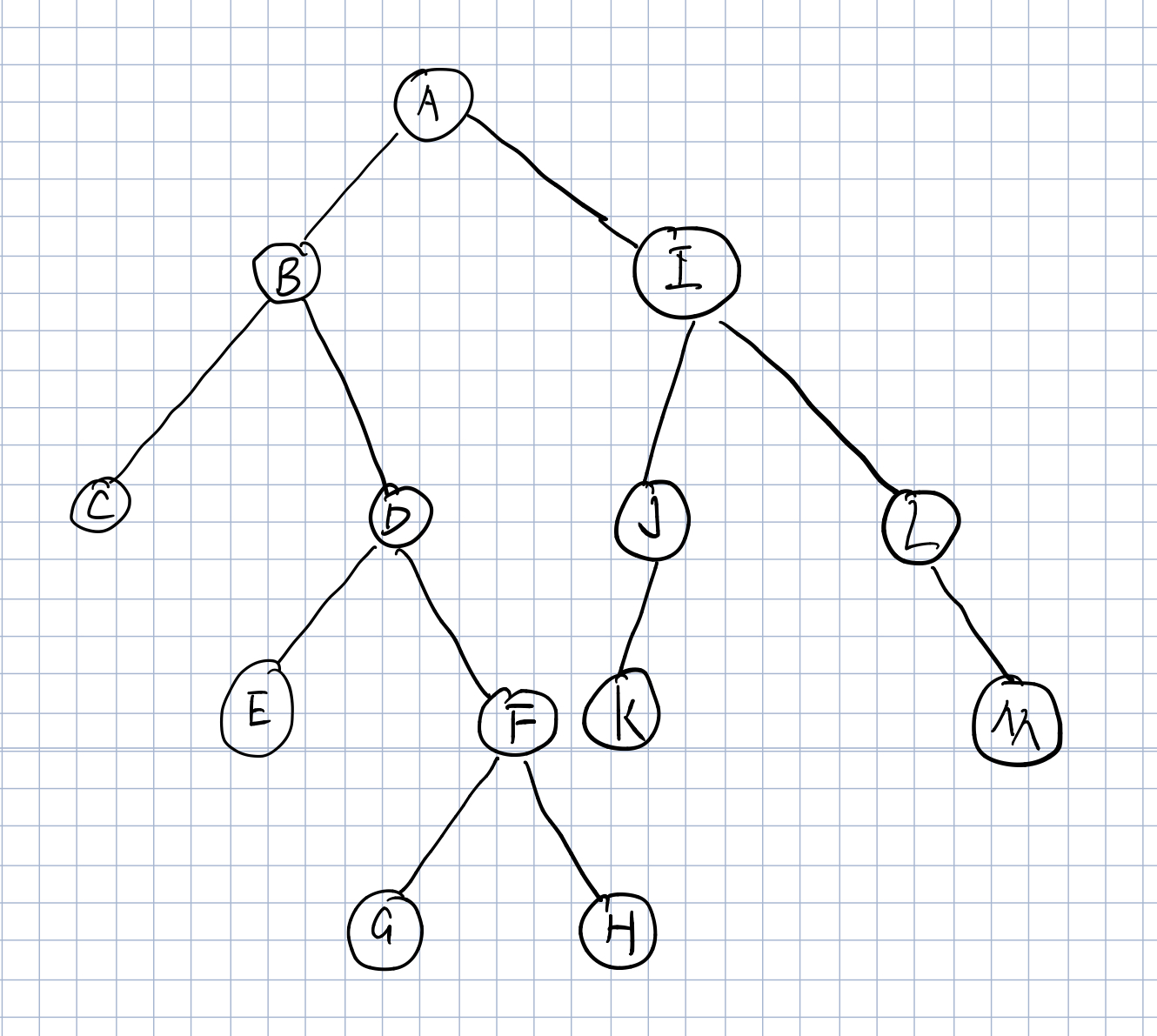
先序遍历为:

ABCDEFGHIJKLM

中序遍历为

CBEDGFHAKJILM

后序遍历为

CEGHFDBKJMLIA

0x03 森林

森林为n课不相交的树,其存储表示为

typedef struct CSNode{
    ElemType          data;
    struct CSNode     *firstchild, *nextsibling;
}CSNode,*CSTree;

森林转换成二叉树

如果F={T1,T2,...,Tn}是森林，则可按照如下规则转换成一颗二叉树

  1. 若F为空，即m=0,则B为空树
  2. 若F非空,即m!=0,则B的根root即为森林中第一棵树的根ROOT(T1);B的左子树LB是从T1中根节点的子树森林F1={T11,T12,...,T1m1}转换而成的二叉树;其右子树RB是从森林F'={T1,T2,...,Tm}转换而成的二叉树

二叉树转换成森林

如果B={root,LB,RB}是一棵二叉树，即可按如下规则转换成森林F={T1,T2,...,Tn}

  1. 若B为空，则F为空
  2. 若B非空，则F中第一棵树T1的根ROOT(T1)即为二叉树B的根root;T1中根结点的子树森林F是由B的左子树LB转换而成的森林;F中除T1之外其余树组成的森林F'={T1,T2,...,Tm}是由B的右子树RB转换而成的森林。

如果为二叉树与森林的对应关系为

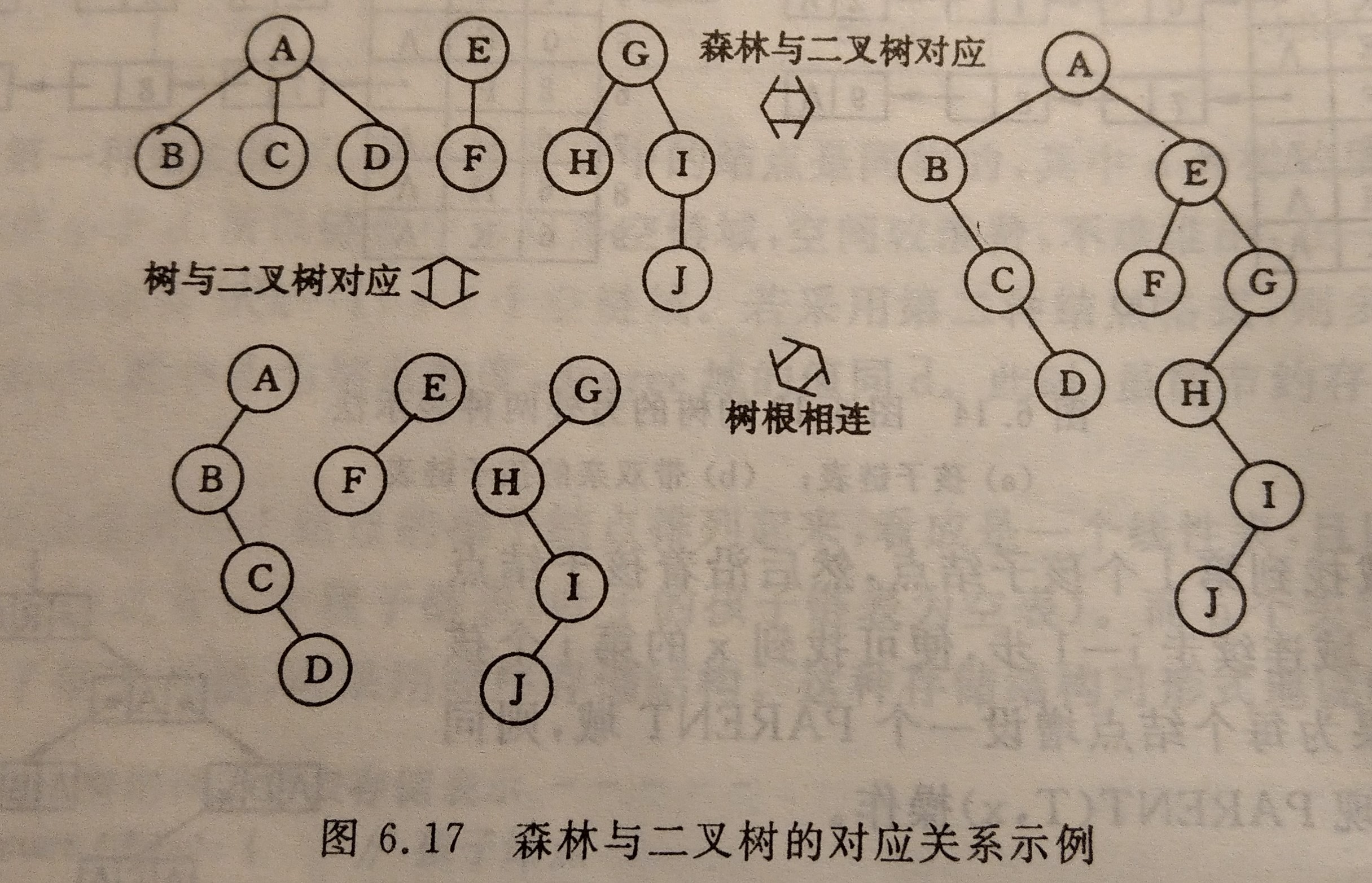
0x04树和森林的遍历

先序遍历森林

若森林非空，则

  1. 访问森林中第一棵树的结点
  2. 先序遍历第一棵树中根结点的子树森林
  3. 先序遍历除去第一棵树之后剩余的树构成的森林

中序遍历森林

若树非空，则

  1. 中序遍历森林中的第一棵树的根节点的子树森林
  2. 访问第一棵树的根结点
  3. 中序遍历除去第一棵树之后剩余的树构成的森林

 

如图6-17结构的先序遍历为

ABCDEFJHIJ

后续遍历为

BCDAFEHJIG

0x05Huffman编码

最优二叉树

从树中一个结点到另一个结点之间的分支构成这两个结点之间的路径，路径上的分支数目称做路径长度。书的路径长度是从树根到每一个结点长度之和。树的带权长度为树中所有叶子结点的带权长度之和，称为WPL

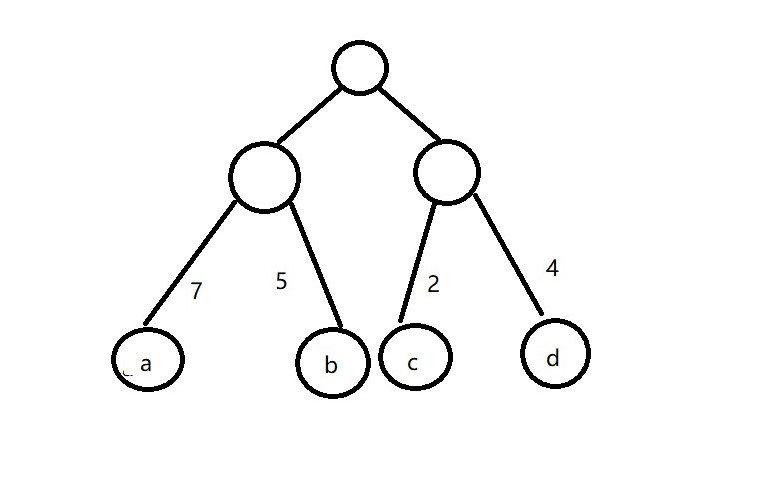
上述的权重为:WPL = 7x2+5x2 + 2x2 + 4x2 = 36

构造Huffman树

  1. 根据给定的n个权值{w1,w2,..,wn}构成n棵二叉树的集合F={T1,T2,..,Tn},其中每棵二叉树T中只有一个带权为wi的根节点，其左右子树均为空。
  2. 在F中选取两个根节点的权值最小的树作为左右子树构造一棵新的二叉树，且置新的二叉树的根节点的权值为其左、右子树上根节点的权值之和
  3. 在F中删除这两棵树，同时将新的到的二叉树加入到F中。
  4. 重复1和2，知道F只含一棵树为止。这棵树为Huffman树

例，有如下一列字符

ADCBDABDCBDBCDCDCD

4个叶子结点ABCD，其权值分别为{2,4,5,7}，可以构造出如下的Huffman树

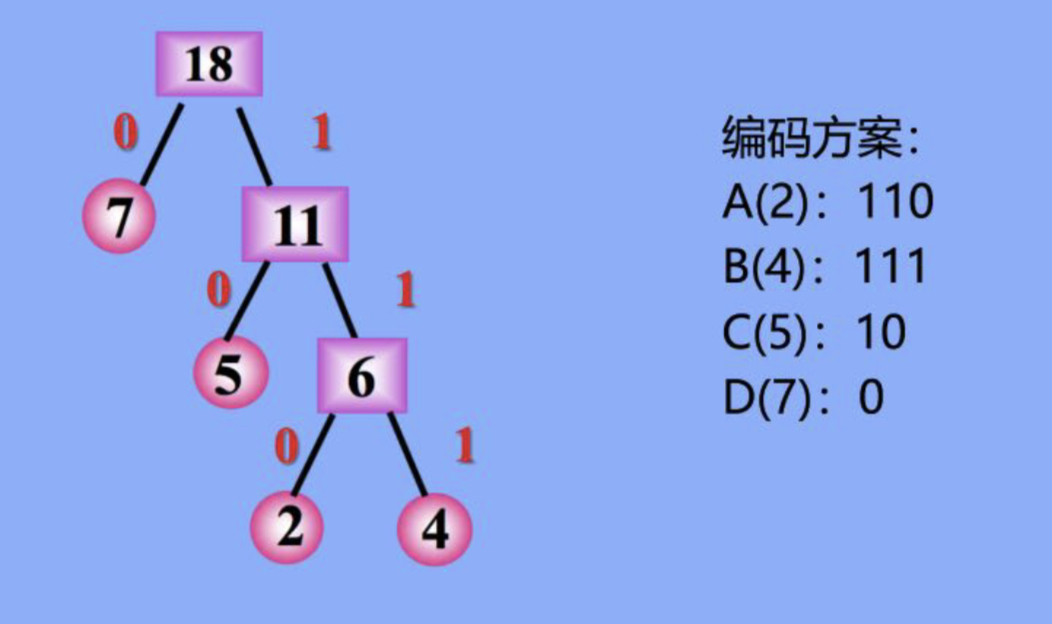
其编码解码代码如下

#include<stdio.h>
#include<stdlib.h>
#include<malloc.h>
typedef struct{
	unsigned int weight;
	unsigned int parent,lchild,rchild;
}HTNode, *HuffmanTree;

typedef char **HuffmanCode;

int Select(HuffmanTree &HT, int n, int &s1, int &s2)
{
	int i,min,count=1;
	while (count < 3) {
		min = 2000;
		for (i = 1; i <= n; i++)
		{
			if (HT[i].parent == 0 && min > HT[i].weight)
			{
				if(count==1) s1 = i;
				else{
					if (i == s1) continue;
					s2 = i;
				}
				min = HT[i].weight;
			}
		}
		count++;
	}
	return 0;
}

void HuffmanCoding(HuffmanTree &HT, HuffmanCode &HC, int n, int m)//n是Huffman数结点总数，m是待编码字符串的长度 
{
	char *cd;//cd用来存放每个字符的编码 
	int i, start, c, f;
	HC = (HuffmanCode)malloc(sizeof(char *)*(m));//指针数组 
	cd = (char *)malloc(n * sizeof(char));//最长的编码长度为n-1 
	cd[n - 1] = '\0';
	for (i = 0; i < m; ++i)//数据全部存储在叶子结点，所以从叶子结点到根结点反向获取编码；一共有m个字符需要编码 
	{
		start = n - 1;
		for (c = i + 1, f = HT[c].parent; f != 0; c = f, f = HT[f].parent)//从叶子节点出发 
		{
			if (HT[f].lchild == c)//第f个结点的左子结点的下标和c相同 
				cd[--start] = '0';
			else
				cd[--start] = '1';
		}
		HC[i] = (char *)malloc((n - start) * sizeof(char));
		strcpy(HC[i], &cd[start]);
	}
	free(cd);
}

void CreatHuffmanTree(HuffmanTree &HT, int n)
{//建立Huffman树 ，n是叶子节点数。 
	int m, s1, s2, i;
	if (n <= 1)
	{
		printf("字符过少,请重新输入\n");
		return;
	}
	m = 2 * n - 1;//共有m个节点；
	HT = (HuffmanTree)malloc(sizeof(HTNode)*(m + 1)); //从下标1开始，所以总长度+1 
	
	for (i = 1; i <= n; ++i)//将输入字符的各个权重存储进HT数组 
	{
		HT[i].weight = fre[i - 1];
		HT[i].parent = 0;
		HT[i].lchild = 0;
		HT[i].rchild = 0;
	}
	
	//for (i = 1; i <= n; i++) *(HT+i) = { fre[i - 1],0,0,0 };  error C2397
	for (; i <= m; ++i)//i=n+1  
	{
		HT[i].weight = 0;
		HT[i].parent = 0;
		HT[i].lchild = 0;
		HT[i].rchild = 0;
	}
	
	//for (; i <= n; i++) HT[i] = { 0,0,0,0 }; error C2397
	for (i = n + 1; i <= m; ++i)//Huffman树 
	{
		Select(HT, i - 1, s1, s2);
		HT[s1].parent = i;
		HT[s2].parent = i;
		HT[i].lchild = s1;
		HT[i].rchild = s2;
		HT[i].weight = HT[s1].weight + HT[s2].weight;
	}
}

void HuffmanDecode(HuffmanTree HT, int n, char decode[], int len)//形参分别为霍夫曼树，霍夫曼树的叶子节点数，待编译的编码，以及编码的长度 
{

	int m, p, i = 0;
	m = 2 * n - 1;
	p = m;//根结点的位置 
	printf("译码为：");
	for (i; i < len; i++)
	{
		if (decode[i] == '0')
		{
			p = HT[p].lchild;//左儿子节点 
		}
		else
		{
			p = HT[p].rchild;//右儿子节点 
		}
		if (!HT[p].rchild && !HT[p].lchild)
		{
			putchar(letter[p - 1]);
			p = m;
		}
	}
	putchar('\x0a');

}

最后来看一个题目

请实现一个函数，用来判断一棵二叉树是不是对称的。如果一棵二叉树和它的镜像一样，那么它是对称的。，比如

二叉树[1,2,2,3,4,4,3] 是对称的

    1
   / \
  2   2
 / \ / \
3  4 4  3

让如下[1,2,2,null,3,null,3]则不是

   1
   / \
  2   2
   \   \
   3    3

二叉树结构如下

struct BinaryTreeNode

{

  int                               m_nValue;

 BinartTreeNode*    m_pLeft;

 BinartTreeNode*    m_pRight;

};

代码如下

bool isSymmetrical(BinaryTreeNode* pRoot){
	return isSymmetrical(pRoot, pRoot);
}

bool isSymmetrical(BinaryTreeNode *pRoot1, BinaryTreeNode *pRoot2)
{
	if(pRoot1==nullptr && pRoot2 == nullptr) return true;
	if(pRoot1 == nullptr || pRoot2 == nullptr) return false;
	if(pRoot1->m_nValue!=pRoot2->m_nValue) return false;

	return isSymmetrical(pRoot1->m_pLeft,pRoot2->m_pRight) && isSymmetrical(pRoot1->m_pRight, pRoot2->m_pLeft);
}

 

Referebce

  1. 数据结构(C语言版) 清华大学出版社

 

 

 上一页

ctf